Zhanghao

Zhanghao

Alea iacta est.

Sitemap

A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.

Pages

Posts

SOC Matrix Element in DFT

2 minute read

Published:

SOC in DFT

We start from this formula of SOC expression in DFT: \(H_{SOC}=\sum_i\xi_i(r)\vec{L}_i\cdot\vec{S}_i\)

notes on Large Deviation Principle

4 minute read

Published:

Large Deviation Principle

Definition:

The large deviation principle defines a rate function $I(\mathbf{x})$ that: \(\lim_{n\to\infty}-\frac{1}{n}\ln p(\mathbf{x})=I(\mathbf{x})\)

Hubbard Model and Gutzwiller

less than 1 minute read

Published:

Hubbard Model

The one-band Hubbard Model is the simplest model for the interactive electrons in solid.

notes on Wannier Tight-Binding Method

1 minute read

Published:

The Wannier Function is the Fourier transform of the bloch functions. Since bloch function have a gauge freedom, that one can choose a phase function that is periodic in K space and won’t change the bloch function’s functionality, so the wanneir function can be formed in varies ways.

notes on Density Functional Theory (DFT)

less than 1 minute read

Published:

About local and non-local functional: https://physics.stackexchange.com/questions/121816/local-versus-non-local-functionals variation of functionals: Mathematical Physics p.1051 deduction from many body electronic potential to hatree potential and exchange energy. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Advanced_Theoretical_Chemistry_(Simons)/06%3A_Electronic_Structure/6.03%3A_The_Hartree-Fock_Approximation

Quantum Mechanics Notes: Quantization of Angular Momentum

less than 1 minute read

Published:

The present chapter is the first in a series of four Chapters (VI, VII, IX and X) devoted to the study of angular momenta in quantum mechanics. This is an extremely important problem, and the results we are going to establish are used in many domains of physics: the classification of atomic, molecular and nuclear spectra, the spin of elementary particles, magnetism, etc… - Quantum Mechanics Volume 1 (Cohen-Tannoudji)

Classical Mechanics Notes: The Central Force Problem

3 minute read

Published:

As an example, the central force problem used all knowledge of the basic principles in classical mechanics, which is a good practice to review all knowledge that have learnt in the first two chapters of Classical Mechanics (Goldstein)

Physics Notes: Angular Momentum, Magnetic and Spin

1 minute read

Published:

The note is summarized from several good textbook, includes Goldstein’s ‘Classical Mechanics’, Griffiths’s ‘Introduction to Electrodynamics’ and Cohen’s ‘Quantum Mechanics Volume 1’

Relativistic Derivation of Spin Physics: Dirac Equation and spin-orbital coupling

6 minute read

Published:

“The theory of fermions is one of the great triumphs of twentieth-century physics. Most of the credit belongs to Paul Dirac, who started, like Einstein, with some simple assumptions and laid the foundations for the Pauli exclusion principle of chemistry, Fermi statistics in solids, and antimatter in particle physics.”

Deduce the Dirac equation

The basic problem of Schrodinger equation is it doesn’t contain relativistic effect, since if we wrote: \(\begin{align*} i\hbar \frac{\partial}{\partial t}\psi=H\psi=\left[\frac{-\hbar^2\nabla^2}{2m}+U\right]\psi \end{align*}\) we can see the kinetic terms is not relativistically invariant. The conserved quantities in special relativity is $E^2=(mc^2)^2+(cp)^2$. However, if the time derivitive term has second order. Then the equation will become like: \(\begin{align} \left(i\hbar\frac{\partial}{\partial t}\right)^2\psi&=-\hbar^2\frac{\partial^2}{\partial t^2}\psi\\ &=\left[m^2c^4+c^2(-\hbar^2\nabla^2)\right]\psi\\ &=E^2\psi\\ \Leftrightarrow -\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\psi&=\frac{m^2c^2}{\hbar^2}\psi-\nabla^2\psi \end{align}\) There will be two problem appears:

  1. Since this equation is second order, the zero and first order term of $\psi$ can be designed arbitrarily, therefore, the $\psi$ lost it’s physical intepretation where it’s amplitude equals the probability.

portfolio

Back to Tianjin !

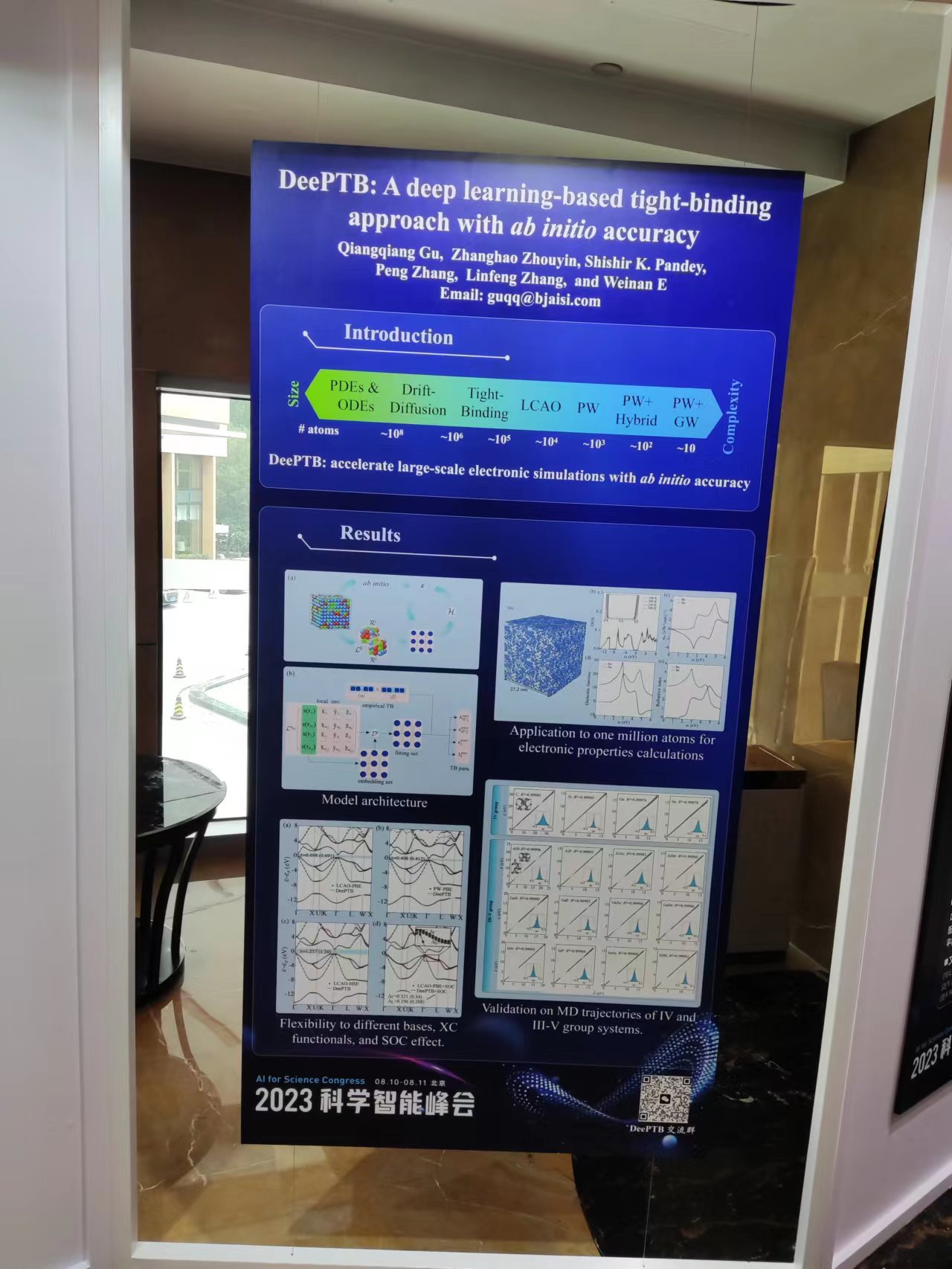
Tianjin has become a second home to me, a serene city where everyone relishes their own pace and finds peace.

publications

AD-NEGF: an End-to-end Differentiable Quantum Transport Simulator for Sensitivity Analysis and Inverse Problems

Published in arxiv, 2022

We implement a quantum transport simulator based on Non-equilibrium Green’s Function with PyTorch, and customly design the gradient computation.

Recommended citation: Zhou, Yingzhanghao, et al. "AD-NEGF: An End-to-End Differentiable Quantum Transport Simulator for Sensitivity Analysis and Inverse Problems." arXiv preprint arXiv:2202.05098 (2022). http://floatingCatty.github.io/files/2202.05098.pdf

talks

teaching